Obiettivo delle attività sperimentale era la verifica quantitativa della legge di diffrazione della luce tramite reticoli di fenditure con diversa spaziatura. Oltre alla verifica della legge, obiettivo dell’esperienza era anche determinare la lunghezza d’onda delle sorgenti luminose impiegate.

La legge fisica da verificare è la seguente:

• l è la lunghezza d’onda della luce emessa da una sorgente laser (sorgente monocromatica coerente), obiettivo finale della misura;
• d è la spaziatura delle fenditure del reticolo di diffrazione (numero di fenditure/mm);
• k è l’ordine della frangia di diffrazione (numero intero);
• sin(q_d,k) è il seno dell’angolo formato dalla direzione del raggio della frangia luminosa di ordine k rispetto alla direzione del raggio incidente (k = 0).

Disposizione sperimentale

Per la verifica delle legge occorre misurare a) diverse lunghezze d’onda, b) diverse spaziature del reticolo e c) diverse frange di diffrazione, a parità di lunghezza d’onda e reticolo. Siccome la legge ipotizza che la lunghezza d’onda l dipenda linearmente da 1/d e da k, per ciascuna lunghezza d’onda (cioè per ciascuna sorgente) abbiamo bisogno di raccogliere almeno 3 valori  per la verifica della dipendenza da 1/d ed altrettanti per la verifica della dipendenza da k.

Nel nostro esperimento abbiamo utilizzato :

• 2 sorgenti laser, una rossa e una verde
• 4 reticoli differenti, con d = 80, 100, 300 e 600 (fenditure/mm)
• Un telaio di supporto allo schermo e al reticolo
• Uno schermo composto da un regolo graduato

In ciascuna prova, per ogni combinazione di laser e reticolo, abbiamo deciso di misurare la posizione di almeno 3 frange (k = 1, 2, 3), da cui ricavare il relativo angolo q_d,k .

Piano delle prove

Il piano delle prove da eseguire è la tabella qui a fianco. Consiste di 8 prove (2 laser x 4 reticoli), con 3 misure per ciascuna prova, corrispondenti a k = 1, 2, 3.

Le colonne a e b del foglio Excel sono state predisposte per raccogliere le misure da eseguire. Esse sono:

• a è la distanza, misurata sul regolo che fa da schermo, tra la frangia k e la frangia del raggio non diffratto;
• b è la distanza tra il reticolo e il regolo che fa da schermo.

Entrambe le misure sono espresse in centimetri.

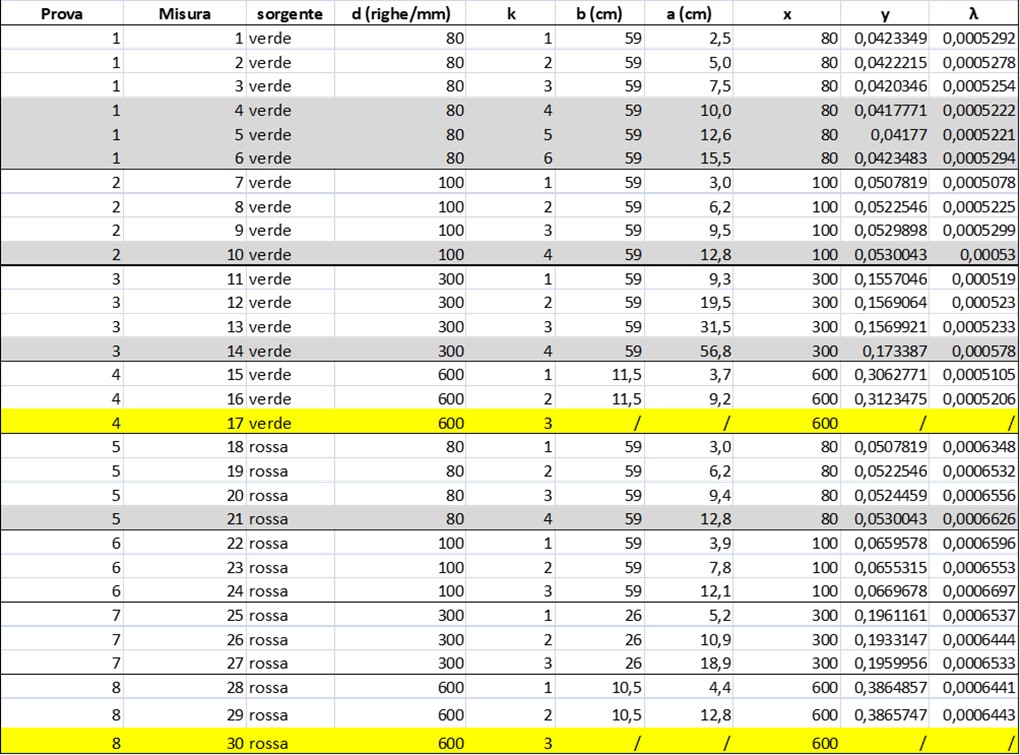
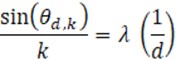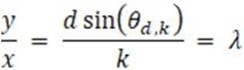Dati raccolti

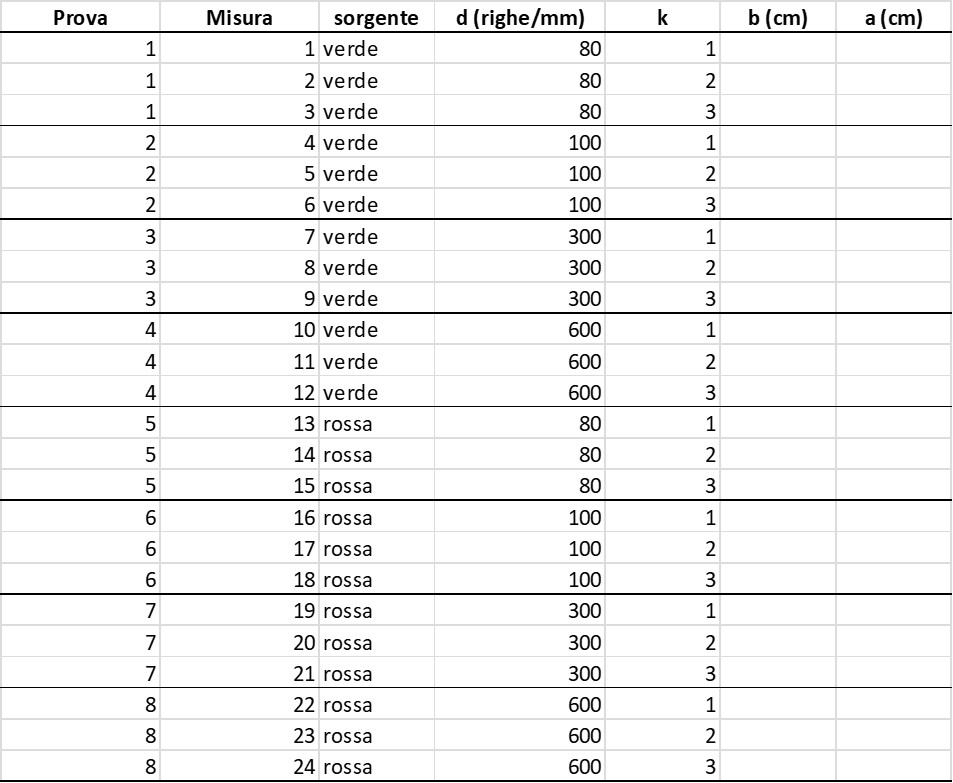
Notiamo anzitutto che in alcune prove abbiamo potuto rilevare dei dati per k = 4, 5, 6 che non erano stati pianificati ma che sono risultati disponibili per l’esperimento.  Inoltre, in altre prove, i dati corrispondenti a k = 3 non sono disponibili poiché l’immagine della frangia usciva dal sistema.  Nella tabella sono segnati in grigio  i dati raccolti che non erano stati pianificati, in giallo i dati pianificati che non abbiamo potuto misurare.

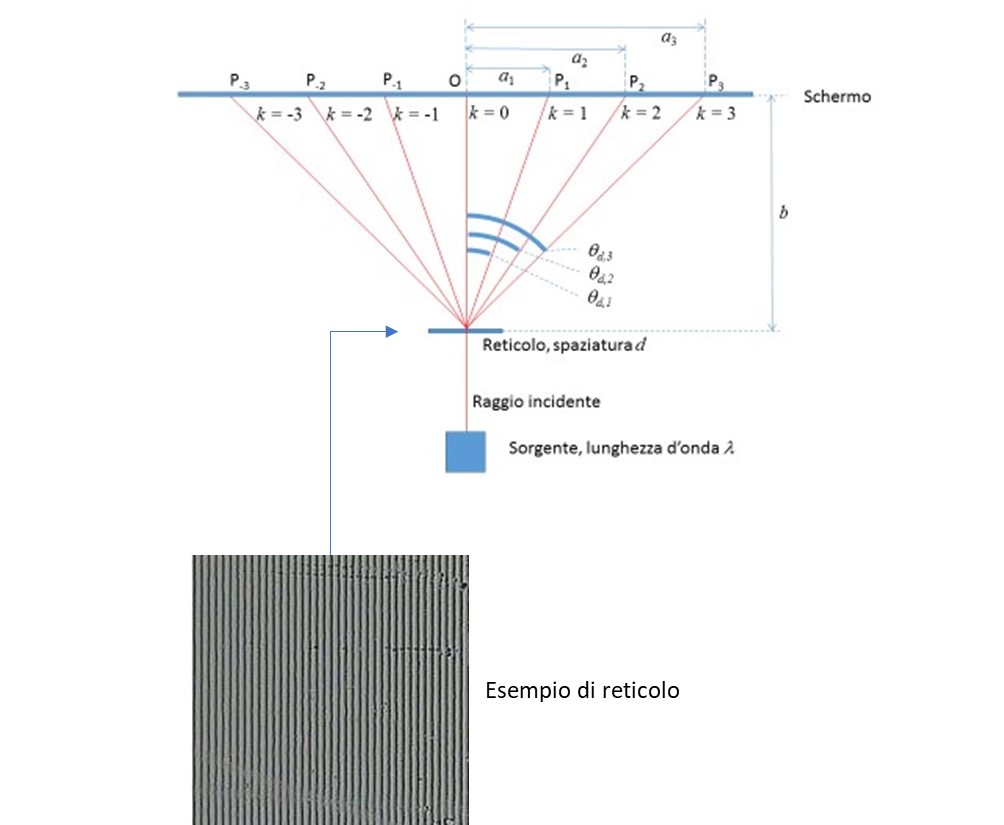
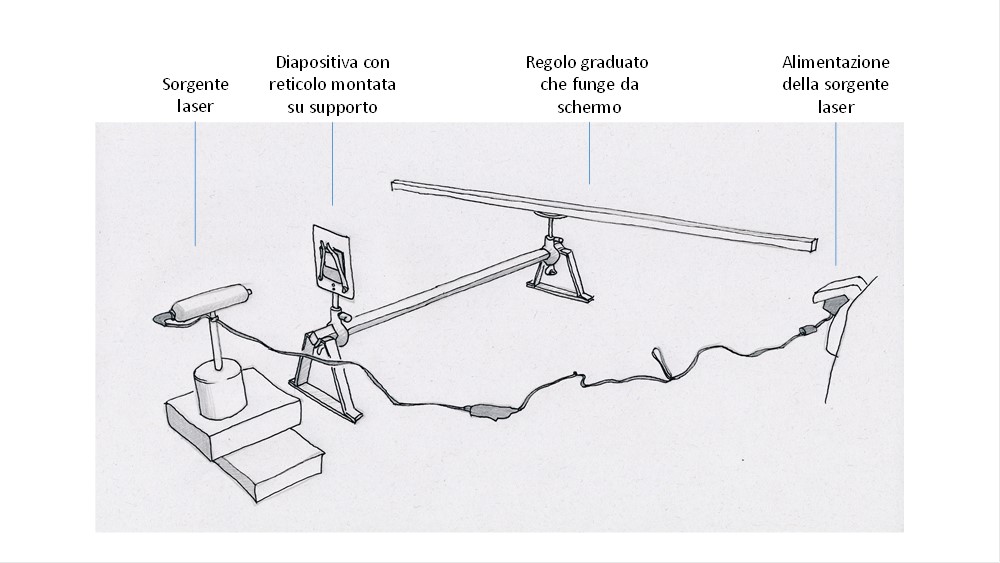
Le misure inserite nel foglio Excel sono anzitutto i valori di a e b misurati direttamente. A partire da questi, sono stati ricavati poi i dati nelle colonne a sinistra, nel seguente modo.

Tramite il teorema di Pitagora, è possibile calcolare sin(q_d,k) mediante la formula:

sin(q_d,k) = a/√(a² +b² )

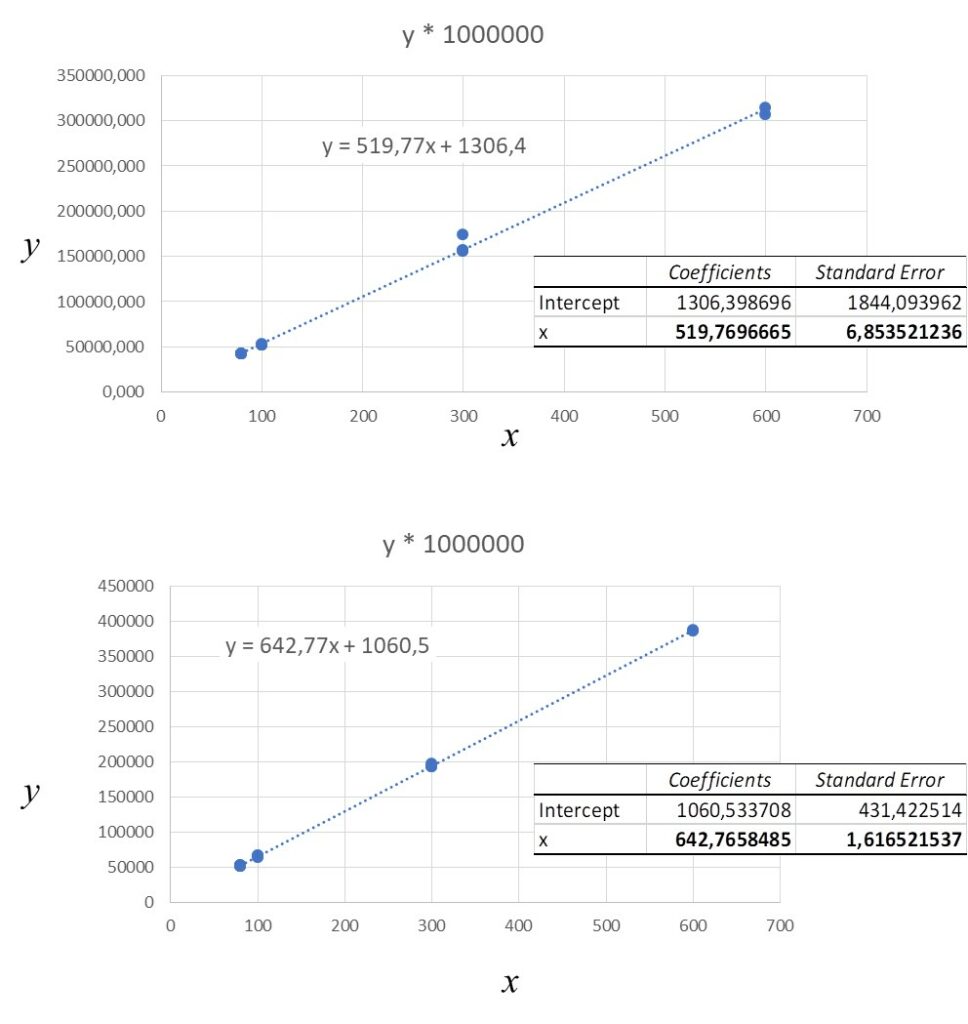
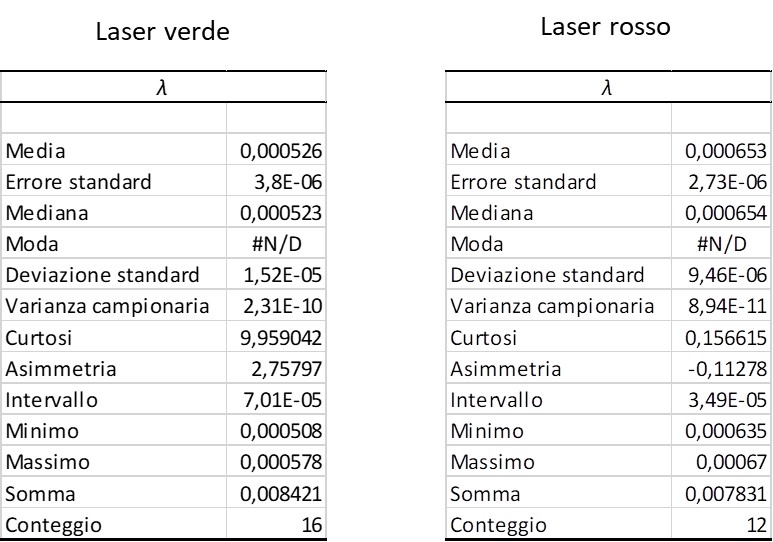
Successivamente abbiamo calcolato le variabili  x, y dalle seguenti formule:  y = sin(q_d,k)/k   e   x = (1/d). Dai valori di x e y e dalla legge dei reticoli, si ricava poi il valore della lunghezza d’onda l, tramite la formula:

Notiamo che questa formula può essere scritta come y = l x, o anche come y = m x + q , dove m = l e q = 0. In pratica, la lunghezza d’onda l è il coefficiente angolare della retta descritta da y in funzione di x.

Analisi di regressione

La analisi di regressione consiste nella costruzione della retta y = m x + q , dove m = l e q = 0.

I grafici mostrano che la dipendenza lineare è verificata molto bene dai dati raccolti, il che permette di validare la forma della legge dei reticoli.

Inoltre, dal coefficiente angolare delle due rette si ricava la stima delle due lunghezze d’onda.

In sintesi, trasformando i dati da mm a nm:

• Laser verde: l = 519,7 nm +/- 2 x 6,8 nm
• Laser rosso: l = 642,7 nm +/- 2 x 1,6 nm

Statistiche descrittive

La analisi tramite statistiche descrittive consiste nella elaborazione delle statistiche (valore medio, deviazione standard, standard error,…) dei singoli dati di lunghezza d’onda della sorgente verde e della sorgente rossa ricavati nella tabella dei dati, colonna l.

Le lunghezze d’onda sono misurate in millimetri (mm). In sintesi, trasformando i dati da mm a nm:

• Laser verde: l = 526 nm +/- 2 x 3,8 nm
• Laser rosso: l = 653 nm +/- 2 x 2,7 nm

I dati di riferimento delle sorgenti laser, forniti dal costruttore,  sono i seguenti:

• Laser verde: l = 532 nm +/- 1 nm
• Laser rosso: l = 650 nm +/- 5 nm

Esperienze di laboratorio

Introduzione alla statistica